Alright folks, let’s dive into something I’ve been wrestling with lately: proving Big O notation. It’s not always straightforward, and I figured sharing my process might help someone else out there.
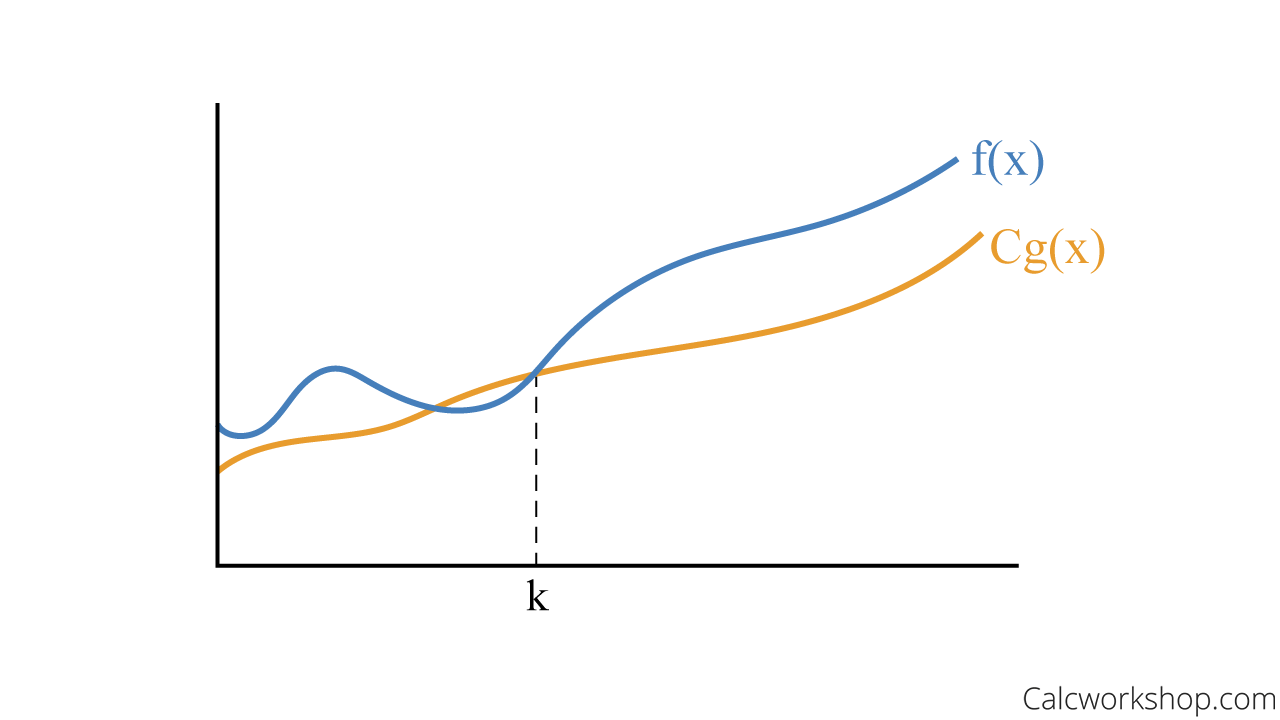
So, I started with the basics. I knew that Big O is all about the upper bound of an algorithm’s growth rate. The goal is to find a function that our algorithm’s runtime will never exceed, eventually. That “eventually” part is key.
First up, I grabbed a simple piece of code. Let’s say we have this:
- Looping through an array once.
Okay, pretty basic. Now, the challenge: how do we prove that this is O(n)? We can eyeball it and say, “Yeah, it touches each element once, so it’s linear.” But where’s the actual proof?
Step 1: Break It Down
I started by identifying the operations. Each iteration of the loop does a few things: array access, comparison, incrementing the counter. We can say each of those takes constant time, let’s call it ‘c’.

Step 2: Find the Constant ‘c’ and ‘n0’
This is where things get interesting. We need to show that there exist constants ‘c’ (a multiplier) and ‘n0’ (a starting point) such that for all n > n0, our algorithm’s runtime T(n) is less than or equal to c f(n), where f(n) is the Big O function we’re trying to prove (in this case, n).
Let’s assume each operation inside the loop takes ‘c’ time, and the loop runs ‘n’ times. The total runtime T(n) can be represented as T(n) = a n + b, where ‘a’ represents operations inside the loop, and ‘b’ is the outside.
Now the fun part begins. We need to prove that T(n) n0
Step 3: Find ‘c’ and ‘n0’

My initial thought was “How the heck do I find those constants?”. After tinkering around and writing out some inequalities, here’s what I did.
I started with the requirement T(n) <= c n. Let's assume T(n) = 5 n + 10 (a=5, b=10).
We need to find c and n0 such that 5 n + 10 <= c n.
Let’s choose c = 10. Now the expression changes to 5 n + 10 <= 10 n. Simplify, 10 = 2.
So, we have c=10 and n0=2.

This means that for all ‘n’ greater than 2, the runtime T(n) will never exceed 10 n. Which is what we wanted.
Step 4: Formalize It (A Bit)
To make it sound “official,” you’d say something like:
Given the runtime of T(n) = 5 n + 10, we can choose c = 10 and n0 = 2, such that for all n > 2, T(n) <= c n. Therefore, the algorithm is O(n).
Takeaways
- Big O is about eventual behavior. Don’t get hung up on small input sizes.
- Proving Big O involves finding those constants ‘c’ and ‘n0’. It’s a bit of an art sometimes.
- Start with simple algorithms and work your way up.
Important Conclusion
It can be a tedious process. But at the end of the day, it’s a valuable skill. Happy coding!