Alright, let’s dive into this little math problem I tackled today: “two thirds divided by three.” Sounds simple, right? Well, sometimes the simplest things can be surprisingly insightful. Here’s how I went about it.
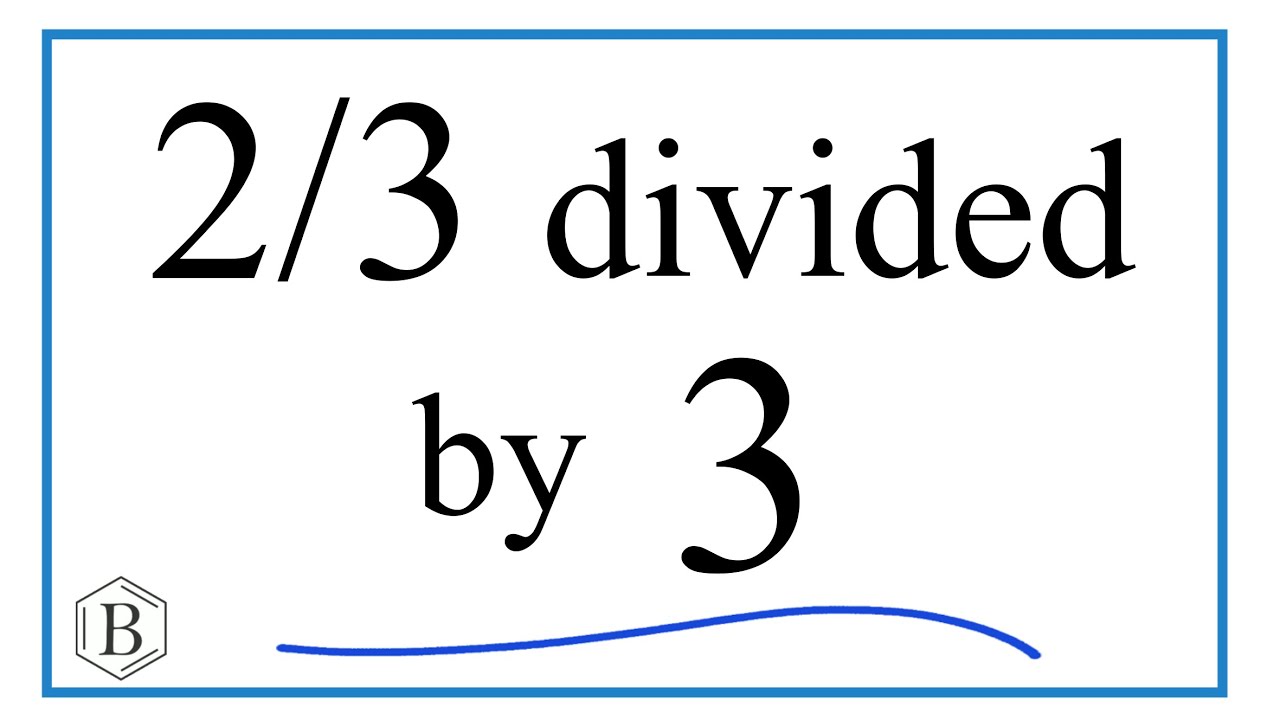
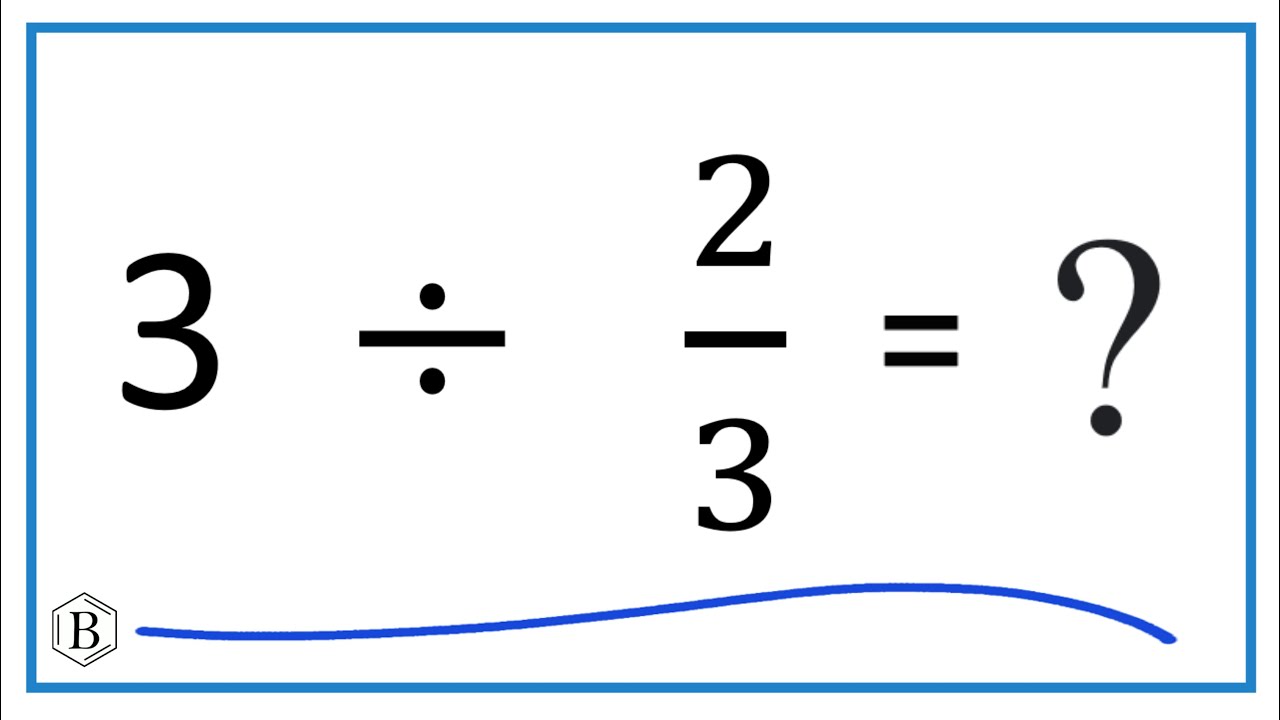
First things first, I wrote it down. Always a good starting point. So, I had 2/3 ÷ 3. Now, I remembered back to my school days, something about dividing by a whole number being the same as multiplying by its reciprocal.
Okay, so the reciprocal of 3 is 1/3. That meant the problem transformed into something a little more manageable: 2/3 1/3. I remembered how to do this. You just multiply the numerators and denominators.
So, 2 1 = 2, and 3 3 = 9. That gave me 2/9. I was like, “Okay, cool, I think I got it.” Just to double check myself, I pulled up a calculator (no shame in that!).
Typed in 2/3, then the division symbol, then 3. Hit equals, and boom! 0.222222… Now, I knew that 2/9 as a decimal is 0.222222… too, so I was pretty sure I got it right!
But here’s where it got interesting for me.
I started thinking about why this works. Why does dividing by a number become multiplying by its reciprocal? I figured I would try and visualize the two thirds, i.e. 2/3.
- Imagine a pie cut into three slices, each piece is 1/3.
- Imagine you have 2 of these pieces, i.e. 2/3, now you want to divide it by 3.
- Visually you are dividing each of the 2 pieces into 3 smaller pieces. That means each original piece is now 1/3 of its original size. So 1/3 1/3 = 1/9.
- You are left with six pieces, and each piece is 1/9 of the entire pie. Now you have six 1/9 pieces, which is the same as 6/9. But since you originally had 2 pieces, you divide 6 by 3, which gives you 2. So your answer is two 1/9 pieces, i.e. 2/9.
It wasn’t just about getting the right answer. It was about understanding the math.
It’s a good reminder that even the simplest math problems can lead to deeper understanding if you take the time to really think them through.